Matemática: Adição e subtração de frações

Existem situações cotidianas que, se afastadas do conhecimento matemático, nos parecem impossíveis, irreais. Porém, quando nos vestimos com a camisa da mais antiga das ciências (matemática) parece nos clarear o horizonte nebuloso visualizado outrora.

“Marcos gastou (três décimos) do seu salário com diversão”

“75% () dos royalties do petróleo serão destinados à educação”

Ao representarmos um número inteiro utilizamos o conjunto dos números inteiros (Z), ou seja, Z = {..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}. Neste trabalho estudaremos a adição e subtração de partes do inteiro: as frações. O cálculo da soma ou subtração entre frações é possível da mesma forma como é possível realizarmos a soma entre números inteiros.

Veja também: Adição e Subtração de Frações 3

Adicionando frações com denominadores iguais

Antes de prosseguirmos com a adição (soma) e a subtração de frações, vamos verificar cada parte que as compõe, para obtermos clareza no cálculo e reconhecermos, sem dificuldades, as suas nomenclaturas.

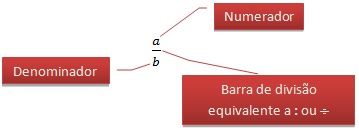
Para calcular a soma entre duas frações com denominadores iguais, conservamos um denominador e somamos os numeradores.

Exemplo 1

Adicione as frações

e entre si.

Solução algébrica

→ conserva o denominador

→ fração soma

Solução geométrica

→

→

→

Para calcular a subtração entre duas frações com denominadores iguais, conservamos um denominador e subtraímos os numeradores.

Exemplo 2

Determine .

Solução algébrica

→ conserva o denominador

→ fração diferença

Solução geométrica

→

→

→

Adição de frações com denominadores diferentes

Para calcular a soma entre duas frações com denominadores diferentes, deve-se encontrar frações equivalentes às frações iniciais, porém com o mesmo denominador, e somar os numeradores.

Exemplo 3

Adriana viajou para a praia. Durante a primeira hora de viagem, ela percorreu do caminho e, na segunda hora, mais . Que fração do percurso total Adriana já percorreu?

Solução

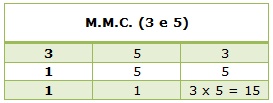
Vamos encontrar frações equivalentes as dadas no problema encontrando o M.M.C. entre 3 e 5.

→ conserva um denominador e soma os numeradores

→ fração soma

Após achar o Menor Múltiplo Comum (M.M.C.) entre os denominadores 3 e 5, dividimos o M.M.C. encontrado pelo denominador da fração inicial e multiplicamos o resultado pelo numerador, também da fração inicial. O resultado é o numerador da fração equivalente. Repetimos esse procedimento para todas as frações do problema em questão.

OBSERVAÇÃO: da mesma forma que na adição de frações com denominadores diferentes, para calcular a subtração entre duas frações com denominadores diferentes, deve-se encontrar frações equivalentes às frações iniciais, porém com o mesmo denominador, e subtrair os numeradores. Se tomássemos como exemplo o exemplo anterior, encontraríamos, da mesma forma, o M.M.C. dos denominadores 3 e 5, que daria 15, dividiríamos 15 pelo denominador e multiplicaríamos o resultado pelo numerador de cada fração inicial, a fim de encontrarmos as frações equivalentes a elas. Em seguida, conservaríamos um denominador e subtrairíamos os numeradores das duas frações.

“Não há começo que não leve a um fim, nem um fim que não leve a um novo começo”. (Robison Sá)

Referências:

PROJETO ARARIBÁ: matemática, v. 1. – 3. ed. – São Paulo: Moderna, 2010.